Expanding Evolutionary Theory Beyond Darwinism with Elaborating, Self-Organizing, and Fractionating Complex Evolutionary Systems

Fichter, Lynn S., Pyle, E.J., and Whitmeyer, S.J., 2010, Journal of Geoscience Education (in press)

---

Elaborating Evolutionary Mechanisms

Resources at bottom of page

Elaborating evolution begins with a seed, an ancestor, or a randomly generated population of agents, and evolves by generating, and randomly mutating, a large diversity of descendants which are evaluated by an external fitness function; those that do not measure up selected out. The fitness function may be a real environment, an abstract environment, or another “species” of agents.

      We talk about biological evolution in terms of changes in the gene pool of a population from generation to generation by such processes as mutation, natural selection, and genetic drift as organisms adapt. Elaborating evolution is characterized by experimentation—lots of experimentation (large numbers of offspring, or many species in a clade); and failure—lots of failure (death and extinction). Indeed, failure is one of the key components of natural selection. Ninety-nine percent of all species that have ever existed are extinct and most individuals born do not survive to reproduce. To maintain this natural selection machine, life has to continuously elaborate, constantly produce new genotypes to experiment with.

     But, biology is not the only example of elaborating evolution. Businesses, for example, behave similarly to living systems as they diversify in an elaborating economy (Beinhocker, 2007), and on average 10% of businesses fail–go extinct–every year (Ormerod, 2007). Indeed, the precise mathematical relationship that describes the link between frequency and size of the extinction of companies is virtually identical to that which describes the extinction of biological species in the fossil record (Ormerod, 2007).

     But, because the units of biological evolution (genes, individuals, species, etc.) are not common to all elaborating evolutionary systems, Darwinian evolutionary theory is not a general theory of evolution, but only a special theory of elaborating evolution.

The General Evolutionary Algorithm

     What is common to all elaborating evolutionary systems is the General Evolutionary Algorithm (GEA) (Beinhocker, 2007):

1) Differentiate - create at random, from an ancestor agent, a large number of "descendents."

2) Select - compare the "descendents" against an external fitness function and select out those that don't measure up,

3) Amplify - reproduce the survivors (thereby, amplifying the traits that survived the selection process), but mutate the offspring at random (creating new diversity that builds on the advances gained by the last generation),

4) Repeat - run the algorithm for as many generations as desired.

Any system that evolves by this process, regardless of the actual units that are differentiating and being selected, is an elaborating evolutionary system. In systems terminology differentiate equals positive feedback (an increase in the amount and diversity of information), while (natural) selection is negative feedback (trimming back of information). Amplify/repeat is equivalent to recursive iteration (feed the result back into the algorithm.) If we apply this to a very simple model of information flow in biological reproduction the GEA works like this (see figure below).

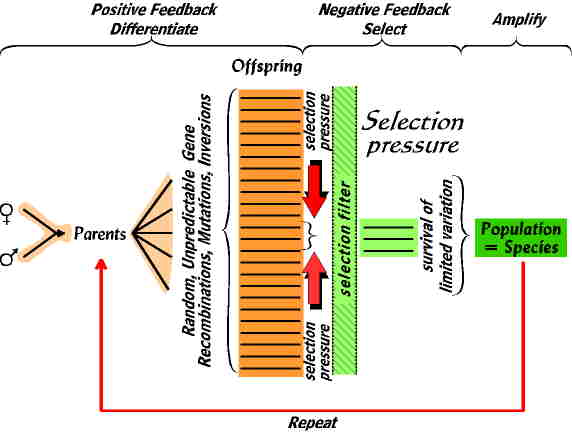
1) Differentiate = positive feedback. Reproduction where genetic recombination, mutations, inversions, etc. result in an increase in information diversity in a large number of offspring.

2) Select= negative feedback. Natural selection where those offspring that deviate too far from the fitness function of the environment are removed.

3, 4) Amplify and repeat are the next reproductive cycle.

WordEvolv, a simple General Evolutionary Algorithm

     An example of a simple non-biological elaborating system that follows the General Evolutionary Algorithm is WordEvolv. The question is, beginning with a random string of letters and spaces can a machine evolve this random string into one that matches a target string of letters and spaces. The process begins by establishing a target string; for example, a phrase, or someone’s name. This becomes the fitness function of the system. Then we run the algorithm.

1) Differentiate = positive feedback. Begin with a random string of letters and spaces the same length as the target string. Reproduce it 20 times mutating at random each of the “offspring.”

2) Select = negative feedback. Compare each of the 20 strings with the target string and calculate how similar they are to the target string (for example, by determining how far away in the alphabet each letter in the string is from what it should be). Keep the one string closest to the target and eliminate the other 19.

3, 4) Amplify and repeat Feed the one surviving best-fit string back into the algorithm, reproduce and mutate it 20 times, etc.

     WordEvolv illustrates the power of the GEA if we calculate how long it would take to generate the target string simply by generating strings at random (the proverbial room full of monkeys with typewriters; eventually one will type out the Gettysburg address.) For the target string, “What is this phrase” there are 2.43 x 10E18 possible strings, which on my computer would take 88,185 years to generate. However, beginning with a random string the same length as the target string, and running it through a differentiate/select/amplify process the target string can be evolved in generally between 50 and 75 generations. A copy of the program is available.

Examples of Elaborating Evolutionary Systems

     This is probably not a complete list, but we can identify three classes of elaborating systems using the GEA.

1. Biology

2. Economic systems

3. Genetic algorithms

     Part of the difficulty with using biological systems as models of elaborating evolution is that biological evolution is messy. There are millions of living organisms, with complexity ranging from simple bacteria to complex eukaryotes, that do not all evolve by the same mechanisms. Bacteria, for example, are known to exchange genes in ways eukaryotes do not, making it difficult to decipher evolutionary relationships. Apparently there is more than one way that biological systems increase in complexity, diversity, order, and/or interconnectedness with time.
     In addition, although we can deduce how elaborating biological systems evolve it is difficult to gather empirical evidence on exactly what genes are doing what, how they are interacting, how the environment is influencing the evolution, etc. It is fair to say that there is so much more we need to learn about biological evolution. On the other hand, many biological processes are the result of self-organizing and fractionating mechanisms and we are further from integrating them into a coherent biological evolutionary theory.
     Economies are probably easier to understand as complex evolving elaborating systems just because there is so much documentation available (although our understanding is severely limited by the traditional equilibrium assumptions that lie behind modern economic theory; see "Beinhnocker, Mandelbrot, Taleb.)

Examples of Genetic Algorithms

     Genetic algorithms is a branch of Artificial Life studies where electronic “ants” are placed into electronic ecosystems and allowed to interact and evolve. Today GA’s are mostly used as a search technique in computing to find exact or approximate solutions to optimization and search problems, but they are also used to model elaborating evolutionary processes.
     From an experimental viewpoint genetic algorithms are the most interesting. Biological evolution is, of course, very complex, and considerable work needs to be done to rethink the evolutionary models we already have in terms of chaos/complex systems. WordEvolv is a very basic elaborating system but much more sophisticated genetic algorithms are available (see Tierra and Avida).
     One of the advantages of studying elaborating evolution with genetic algorithms is that we have access to all the information in the system. For a general model of elaborating evolution we want a system that satisfies at least three criteria:

1) Easy to experiment with, where all the data about matings, mutations, crossovers, etc. are accessible

2) Tunable: we can experimentally play with the variables

3) Can demonstrate the chaos/complex systems universality properties of evolutionary systems.

     Genetic algorithms satisfy all these criteria. This is no substitute, of course, for the study of real biological or economic systems. But, then again mathematical modeling has a long history in biology (from population genetics to ecosystem modeling), and is even more extensively used in economics. The difference is most of these are based on equilibrium principles, while genetic algorithms are complex system models.

Resources

     The theoretical world of non-biological elaborating evolution is mostly contained in the field of Artificial Life (a.k.a Alife), actually a branch of mathematics. An excellent introduction to the subject is Levy (1993), but the world wide web has many sites devoted to the many facets of the subject. Search under artificial life, genetic algorithms, cellular automata, and robotics. The beauty of Alife studies is the ability to create electronic bugs and place them in electronic ecosystems and watch them evolve. These are called genetic algorithms. On the other hand, the behavior of some Alife systems can be explained verbally with great effect. The suggestions below are only a small sampling of what is available.

Wordevolv      The idea for WordEvol comes from a DOS based computer program by Stephen Prata (1993), rewritten by Steve Baedke in a Windows version. A very effective demonstration of how efficiently a mutation/natural selection strategy can evolve a meaningful pattern from a meaningless string of random letters.

John Muir Trail      This genetic algorithm was developed by an MIT research group to discover how efficiently an electronic species could learn to run a trail. It is described by Levy (1993) and Johnson (2002), and we use it to explain the principles of a genetic algorithm.
     An online more technical description is by Jefferson, Collins, and Cooper.

Avida and Tierra
     In these two programs a population of self-replicating computer programs is subjected to external pressures (such as mutations and limited resources) and allowed to evolve subject to natural selection. These systems are as close as we have gotten so far to life in a computer. Avida is the research version, Tierra created by Tom Ray provides downloadable software. As with the John Muir Trail the procedures and outcomes are readily accessible and understandable, and can be easily described.

Ramps/Anti-Ramps
      is an early genetic algorithm developed by Danny Hillis. It is a quintessential example of one of these systems, and a clear example of Red Queen evolution. Levy in Artificial Life discusses it, but we have a link to excerpts of his discussion with additional notes.

Sim Life (as well as Sim Ant, Sim City, and Sim Earth)
     are not just computer games, they are all genetic algorithms that evolve through interactions with the player. The brain child of Will Wright, they evolved out of his early interest in robotics and system dynamics. If you or your students are familiar with these “games” then you have first hand experience with a genetic algorithm.

Floys
     These are available as applets on the WWW. Floys belongs to the realm of flocking Alife systems (called boids). The basic version is only a flocking system and thus belongs technically a self-organizing system, but there is available at the same site a version that evolves as a genetic algorithm.

---

Go on to Self-Organizing Evolution

Go on to Fractionating Evolution

Go on to Rubrics for Teaching Chaos/Complex Evolutionary Systems