(Back to Increasing Instability)     (To Power Laws)

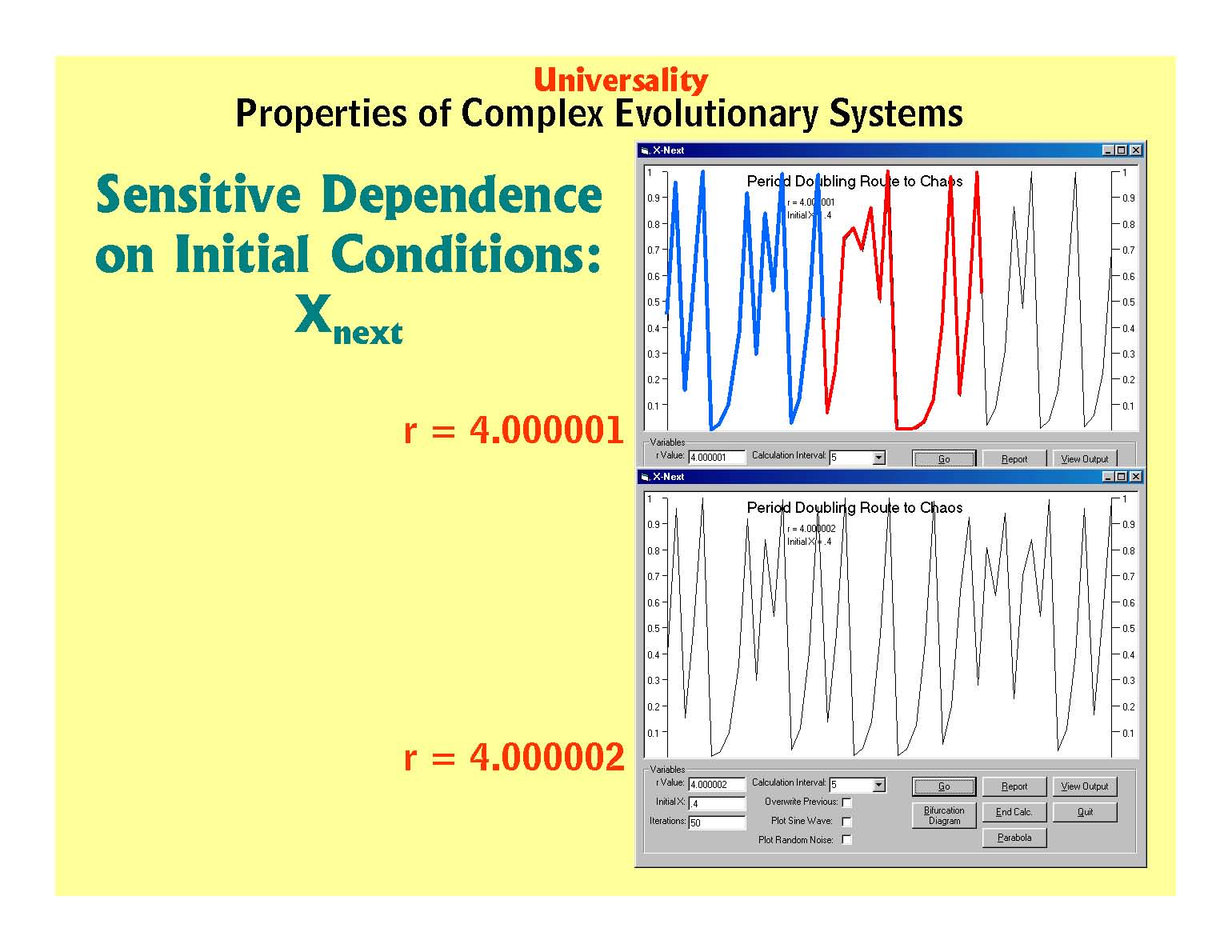
Model: Sensitive Dependence in Time Series Diagrams

Logistic System (Xnext) - Part 2 of 2 Parts

(Part 2 of 2 parts)

Strategies and Rubrics for Teaching Chaos and Complex Systems Theories as Elaborating, Self-Organizing, and Fractionating Evolutionary Systems,

Fichter, Lynn S., Pyle, E.J., and Whitmeyer, S.J., 2010, Journal of Geoscience Education (in press)

---

Description: When we ask students if they are familiar with the butterfly effect, many say they have never heard of it. After some discussion of, for example, the aphorism “The straw that broke the camel’s back,” or the poem that begins “For want of a nail the shoe was lost . . . “, or the movies “The Butterfly Effect” and “Sliding Doors” most will begin to nod knowingly. But, this concept must be sourced back to chaos/complex systems behavior.

Presentation: One simple and quick way to illustrate sensitive dependence is to run the logistic program first at an ‘r’ value of 4.000001, and then open and run another version at 4.000002. In Power Point we animate a line that traces the trajectory on the time series at 4.000001, and then move it to the adjacent time series diagram at 4.000002. It is easy to see the divergence in the trajectories (Power Point). This is quick and easy, but we often go on to spend a little time discussing Edward Lorenz and his discovery of the phenomena (although the mathematician Poincare recognized it around the beginning of the 20th century.)

Anticipated Learning Outcome:

12. In a complex system at high ‘r’ values a difference as little as one part in a million can result in different histories for the system.

---

Power Point

Sensitive Dependence slide from Power Point

Xnext - Logistic System - Computer Model

(Back to Increasing Instability)     (To Power Laws)

---