Binary Eutectic Phase Diagrams

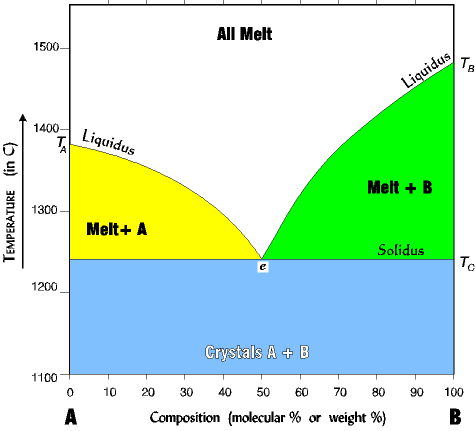
The binary eutectic phase diagram explains the chemical behavior of two immiscible (unmixable) crystals from a completely miscible (mixable) melt, such as olivine and pyroxene, or pyroxene and Ca plagioclase. Here we are going to generalize to two minerals, A and B, or P and Q. We want to observe the behavior of this system under two conditions, one of complete equilibrium during crystallization when all chemical reactions can run to completion, and the second of disequilibrium when fractionation occurs and igneous rocks evolve.

The conventions for the phase diagram include the following (illustration below):

Two immiscible components: such as CaAl2Si2O8 (calcic plagioclase) and FeMgSiO4 (olivine) plotted along the horizontal axis, OR olivine (isolated tetrahedra) and pyroxene (single chain tetrahedra). They are immiscible because they have different crystal structures.

One variable, temperature, plotted along the vertical axis. Pressure is held constant at 1 atmosphere.

Three phases, crystal A, crystal B, and melt.

.Complete miscibility of the melt (magma)

The assumptions are:

The system remains in equilibrium throughout its history so that all reactions can take place and everything can come to stability.

Everything in the original melt remains in communication throughout the crystallization process.

Organization of the Binary Eutectic Phase Diagram

NOTE the following about reading the diagram:

1.   The liquidus line separates the all melt phase from the melt+crystal phase.

2.   The solidus line separates the melt+crystal phase from the all crystal phase.

NOTE that the solidus and liquidus lines are experimental, they have been determined by melting and cooling many melts at different percent compositions.

3.   The eutectic is the point at which all three phases can exist simultaneously, A, B, and melt. The eutectic here is 50% B, but can be any percent depending on the minerals involved.

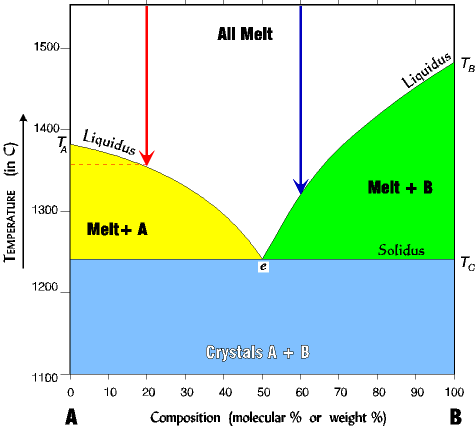
An Example of Crystallization From An Equilibrium Melt With 50/50 Eutectic

1.   For pure A (far left of diagram) the melting (crystalizing) temperature is T_A about 1380^o.

2.   For pure B (far right of diagram) the melting (crystalizing) temperature is T_B about 1485^o.

3.   If we add some B to a melt of A (say 20% B; red arrow) the temperature of melting (crystallization) is lowered to about 1360^o. The more B we add the lower the melting temperature becomes; that is, it moves down the liquidus line toward the eutectic.

4.   Any mixture of A and B lowers the melting (crystallizing) temperature. For example, a mix of 60% B (blue arrow) crystallizes at about 1320^o where pure B crystallizes (melts) at about 1480^o.

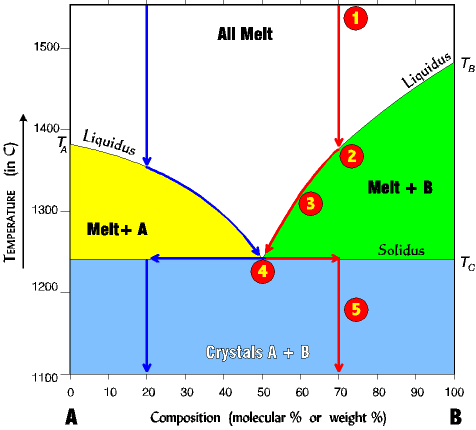
An Example of Equilibrium Crystallization From a Melt With a 50/50 Eutectic

The First Crystal
(numbers on phase diagram correspond with numbers below)
1.    Assume a melt comp- osition of 70% B and 30% A.

2.    Cool melt to liquidus line along red arrow. Only B crystals form at about 1380^o (B is immiscible with A). Only B crystallizes because we are on the Melt+B liquidus line; no A can crystallize until the eutectic is reached.

3.    Removing (crystallizing) B changes the melt composition making in richer in A. Therefore the melt composition begins to migrate to the left, but down the liquidus line toward the eutectic point. The system must stay on the liquidus line since going above it would raise the temperature high enough to melt everything

4.    At the eutectic point, and only at the eutectic point, can A finally begin to crystallize out of the melt, and A and B now crystallize out together at a ratio of 50/50 until all the melt is gone

5.    Finally after all the melt is gone the two crystals A+B can leave the eutectic. Since the original composition of 70% B has not changed we therefore shift the path right to the 70% point, and continue to drop the temperature straight down.
    This path is the same any time the composition of B is greater than the eutectic value. If the composition is less than the eutectic, the path is similar, but a mirror image (see blue arrows for a 20% B).

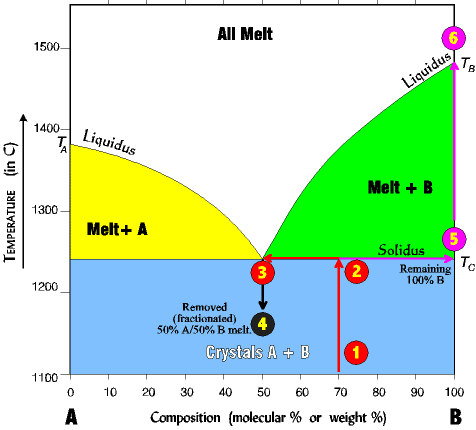
An Example of Melting a Rock With Fractionation And a 50/50 Eutectic

We can reverse the process and begin with a rock, heating it slowly until it melts. In this case the diagram is read the reverse of the crystallization steps (following the numbers below).
1.    Imagine a rock containing 70 % B and 30% A.

2.   It is slowly heated until it reaches the solidus line. At the solidus line the system shifts laterally to the eutectic point.

3.   At the eutectic both components A and B begin melting at the same time in the ratio of the eutectic point (here 50% A/ 50% B). Melting is always at the ratio of the eutectic, regardless of the starting composition. Thus, even though the rock is 70% B and 30% A, the first melt is 50% A and 50% B.

    Melting continues at a 50/50 ratio until all of the least abundant is melted (here A at 30%) and all the remaining unmelted rock is mineral B (which since all of A is melted is now 100% B.)

4.    Now, imagine the process stops just at the point the last crystal of A has melted, and all the melt is removed (fractionated) from the system. A rock with a 50% B/50% A composition will solidify from this melt.

5.    The unmelted rock contains all the remaining mineral B and is thus 100% B and its composition now shifts all the way to the right side, and its melting temperature now becomes that of pure B.

6.    As the temperature continues to rise, B will remain unmelted until the T_B of about 1485^o is reached.

    By this process the original rock has been split into two fractions. There is a melt fraction of 50% A/50% B, and an unmelted (residue) fraction of 100% B. Of course, the separation could occur at any time in the process, before all A has melted, or after A has all melted and some of B as well. The resulting two fractions will differ depending on the circumstances.

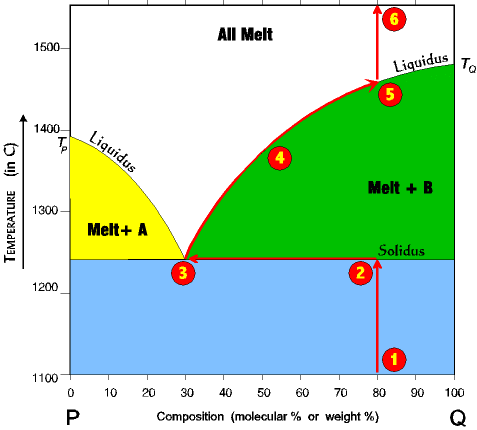
An Example of Melting of a Rock With A 30/70 Eutectic

1.    Imagine a rock containing 60 % Q and 40% P.

2.    It is slowly heated until it reaches the solidus line. At the solidus line the system shifts laterally to the 30/70 eutectic point.

3.    At the eutectic both components P and Q begin melting at the same time in the ratio of 30% P and 70% Q. Melting at the eutectic is always at the ratio of the eutectic, regardless of the starting composition. Thus, even though the rock is 60% Q and 40% P, the first melt is 30% Q and 70% P. Melting continues at a 30/70 ratio until all of the P is melted, and all the remaining unmelted rock is mineral Q (which since all of P is melted is now 100% Q.)

4.    Once all of Q is gone then the system can leave the eutectic. Because Q is the only crystal left, as the temperature rises the system will climb up the Melt+B liquidus.

5.    It climbs up the Melt+B liquidus until it reaches the melting (crystallization) temperature for a 30% Q/70% A system, at which point the last drop of Q melts.

6.    With further rise in temperature the systems just follows the red line up to the top of the diagram.

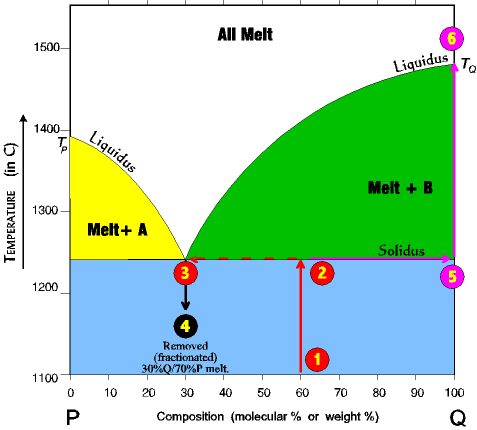
An Example of Fractional Melting of a Rock With A 30/70 Eutectic

This time we will fractionate the system, the first 3 steps are the same as last time but are repeated here.
1.    Imagine a rock containing 60 % Q and 40% P.

2.    It is slowly heated until it reaches the solidus line. At the solidus line the system shifts laterally to the 30/70 eutectic point.

3.    At the eutectic both components P and Q begin melting at the same time in the ratio of 30% P and 70% Q. Melting at the eutectic is always at the ratio of the eutectic, regardless of the starting composition. Thus, even though the rock is 60% Q and 40% P, the first melt is 30% Q and 70% P.

    Melting continues at a 30/70 ratio until all of the P is melted, and all the remaining unmelted rock is mineral Q (which since all of P is melted is now 100% Q.) (Ratios get hard to calculate in a case like this, 60/40 start and 30/70 melting; we will just go along as if it were simple.)

4.    Now, imagine the process stops just at the point the last crystal of P has melted, and all the melt is removed (fractionated) from the system. A rock with a 30% Q/70% P composition will solidify from this melt.

5.    The unmelted rock contains all the remaining mineral Q and is thus 100% Q and its composition now shifts all the way to the right side and its melting temperature now becomes that of pure Q. As the temperature continues to rise it will remain unmelted until the TQ of about 1485o is reached.

    By this process the original rock has been split into two fractions. There is a melt fraction of 30% Q/70% P, and an unmelted (residue) fraction of Q. Of course, the separation could occur at any time in the process, before all Q has melted, or after Q has all melted and some of P as well. The resulting two fractions will differ depending on the circumstances.

Fractional Crystallization

Fractionation can also occur from fractional crystallization. As with fractional melting what is required is separating the crystal from the melt before complete crystallization has occurred.

Give it a try.
See if you understand.

Imagine a system beginning with 15%Q and a 30%P/70%Q eutectic. Cool and fractionate the system until just at the point all the least abundant mineral melts. What is the composition of the two fractions, and at what temperature will this occur? Answer.

Real World Systems:

Simultaneous Solid Solution and Binary Eutectic Fractionation

    Since both miscible (solid solution) and immiscible (binary eutectic) mineral phases exist in a rock, both fractionation processes go on simultaneously as melting occurs. And since in both cases it is the fraction lower on the reaction series which melts preferentially, the effect of both fractionations is to produce a melt which is lower on the reaction series than the original rock.
    The actual fractionation of a rock is more complex than the simple phase diagrams indicate. First, an igneous rock may have 3, 4, 5, or more minerals, all of which interact in complex ways. Second, many phases have partial miscibility and require more elaborate phase diagrams.
    Phase diagrams have been worked out for all the combinations and permutations you can think of:

For three components

For water present

For water absent

For low pressure

For high pressure

But "most rocks are assemblages of phases that require at least four components to describe completely the compositional variation in all phases." (Barker, Igneous Rocks, p 44) The implications of this are that the real world is very complicated, and we do not have an easy time figuring it out.

Go to page on Igneous Rock Evolution

Go to page on Solid Solution Phase Diagram

Go to Igneous Rock Home Page

LSF Home \| Geology Web Sites \| Courses \| JMU Geology
Last Update: 9/29/00	e-mail: (Fichtels@jmu.edu)